O que é notação big-O? Para quer serve? Onde usar? Se você tem dúvidas do que se trata o big-O esse artigo tentará ajudá-lo a esclarecer algo que é fundamental para todo programador e está em seu dia a dia, mesmo que você não saiba.
“Se você acha simples, então você não entendeu o problema direito.”
– Bjarne Stroustrup
O que é o big-O?
É um conceito que descreve o pior caso ou cenário referente a desempenho de um algoritmo, mas o que isso significa? Existem fatores que determinam o quanto um computador irá performar em uma execução de algoritmo, como CPU, memória, disco, tipo de compilação, etc. Como comparar então qual o mais performático algoritmo em relação a outro? O big-O vem para ajudar nisso como uma forma de descrever a taxa de crescimento do tempo de um algoritmo.
A complexidade do tempo
Não vou aprofundar na matemática, mas a complexidade pode ser definida como uma função numérica T(n) onde lê-se tempo em função do número de entradas n. Isso permite medir o tempo como o número de passos, desde que cada passo possua um tempo constante. O big-O representa a função do tempo para a complexidade e tempo de execução de um algoritmo, um exemplo é a representação T(n) = O(n2) que diz que o algoritmo tem uma complexidade de tempo quadrática. Essa anotação é assintótica, ou seja, ela representa o limite do comportamento do custo quando o número de elementos cresce.
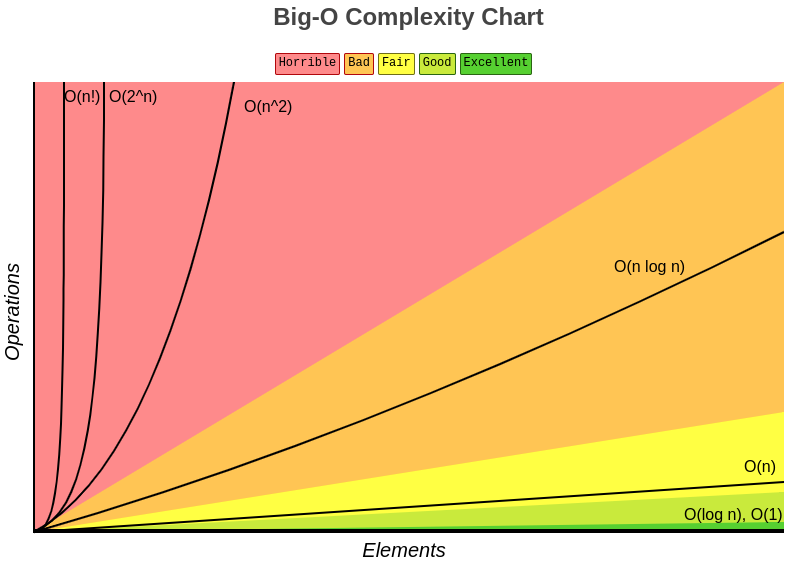
Tipos de classificação por tempo
Os algoritmos podem ser classificados em função da curva de crescimento.
Tempo constante - O(1)
Dizemos que um algoritmo tem tempo constante se independente da quantidade de entradas o tempo não altera. Um exemplo é o acesso a um elemento em um array:
import java.util.Stack
fun main(args: Array<String>) {
val numeros: IntArray = intArrayOf(0, 1, 2, 3, 4, 5, 6, 7, 8, 9)
println(numeros[9])
}
Outros exemplos: adicionar e remover (push e pop) em uma pilha ou fila (enqueue e dequeue).
Tempo logarítmico - O(log n)
Um algoritmo é de execução de tempo logarítmica quando o tempo é proporcional ao tamanho dos dados de entrada. Exemplo é a busca binária:
import java.util.Stack
fun main(args: Array<String>) {
val numeros: IntArray = intArrayOf(0, 1, 2, 3, 4, 5, 6, 7, 8, 9)
println(buscaBinaria(numeros, 0, 9, 4))
}
fun buscaBinaria(numeros: IntArray, esquerda: Int, direita: Int, elemento: Int): Int {
if (direita>=esquerda) {
val meio = esquerda + (direita - esquerda)/2;
if (numeros[meio] == elemento){
return meio;
}
if (numeros[meio] > elemento) {
return buscaBinaria(numeros, esquerda, meio-1, elemento);
}
return buscaBinaria(numeros, meio+1, direita, elemento);
}
return -1;
}
O que significa dizer que a busca binária log de n? Significa que para uma entrada de 16 elementos ele irá executar 4 passos (log 16 é 4) para encontrar o elemento.
Tempo linear - O(n)
Um algoritmo é de tempo linear quando o tempo de execução é diretamente proporcional ao tamanho do dado de entrada, o tempo aumenta linearmente com o aumento dos dados. No exemplo a seguir, um elemento pode ser identificado na primeira iteração e retornado logo, mas o big-O sempre irá assumir o limite superior onde o algoritmo irá percorrer todos os elementos.
import java.util.Stack
fun main(args: Array<String>) {
val numeros: IntArray = intArrayOf(0, 1, 2, 3, 4, 5, 6, 7, 8, 9)
println(temElemento(numeros, 1))
}
fun temElemento(numeros: IntArray, elemento: Int ): Boolean {
for (numero in numeros) {
if(numero == elemento) {
return true
}
}
return false
}
Tempo quadrático - O(n^2)
Quando o tempo de execução de um algoritmo cresce proporcionalmente ao quadrado do tamanho dos dados de entrada, temos um O(n^2). O tempo quadrático é comum em processamentos que possuem iterações dentro de iterações, como um laço for dentro de outro for. Alguns algoritmos bem famosos como selection sort, bubble sort e insertion sort são desse tipo.
import kotlin.collections.listOf
import java.util.Stack
fun main() {
val elementos = listOf("Casa", "Apartamento", "Carro", "Casa")
println(temDuplicatas(elementos))
}
fun temDuplicatas(elementos: List<String>): Boolean {
for (i in elementos.indices) {
for (j in elementos.indices) {
if (i == j) continue
if (elementos[i] == elementos[j]) return true
}
}
return false
}
Tempo exponencial - O(2^n)
Se a cada adição de entrada de dados no algoritmo duplicar o tempo, então temos um tempo O(2^n). Inicialmente a linha de processos é bem próxima da de elementos, mas em pouco tempo sobe bem rápido. Um exemplo clássico é o cálculo recursivo de Fibonacci:
fun main() {
for (i in 0..8) {
print(fibonacci(i))
if (i != 8) print(",")
}
}
fun fibonacci(numero: Int): Int = if (numero < 2) numero else fibonacci(numero - 1) + fibonacci(numero - 2)
Melhor e médio caso
Para a fronteira inferior do gráfico onde está o melhor cenário de tempo é utilizado a notação omega Ω como n2=Ω(n log( n)), também denominado big Omega. Não é muito utilizado para computação, somente para quando se quer atingir o tempo real.
Para o cenário em que se quer saber a complexidade média de execução (algo entre o limite superior e o inferior) é utilizado o termo big Theta. Exemplos:
- 2 n = Θ(n)
- n2 + 2 n + 1 = Θ( n2)
E para quê isso?
No momento de implementar as soluções é importante conhecer esses conceitos para ter uma base para a escolha de determinada técnica. Também pretendo trazer uma série de artigos com os mais diversos algoritmos e o Big-O será utilizado em alguns momentos para ilustrar o desempenho da execução.
Um forte abraço!
Fontes
Big-O Cheat Sheet - https://www.bigocheatsheet.com/